三亚学院信息与智能工程学院吴涛老师之前在科研过程中,读到过一篇很有想象力的论文,借此机会分享给师生们。
在NeurIPS2022大会上,Hinton发表了题目为《TheForwardForwardAlgorithmforTrainingDeepNeuralNetworks》的特邀演讲,具体介绍了他的一些最新关于神经网络的研究。不得不说,大牛是挖坑的,小牛就是填坑的。他提出的FF算法,又开拓了一片新的天地,很有想象力。
Hinton指出,尽管反向传播算法在深度学习领域取得了巨大成功,但作为大脑皮层学习模型,它仍然不可信。没有确凿证据表明大脑皮层传播误差导数或存储神经活动以用于后续的反向传播。也就是说没有明显的证据表明大脑的神经活动有反向传播的过程,且过程中用到了此前的信息。有鉴于此,他提出来一种新颖的前向算法。那具体这个前向算法是什么呢?且听我慢慢道来。
FF(Forward-ForwardAlgorithm)算法:
1. 两个前向传播:一个前向传播称之为PositivePass。这个过程对真实的数据(正样本)进行操作,同时调整权值来完成每一层的增益(increase the goodness)。另一个前向传播称之为NegativePass。这个过程对负样本(negative data)进行操作,同时调整权值以完成每一层的减益(decrease the goodness)
2. 独立的目标函数:每一层都有其独立的目标函数,即对正样本具有高“优度”(goodness),而对负样本具有低“优度”。
3. “优度”的计算:“优度”可以通过多种方式来衡量,例如层中的平方活动之和或负的平方活动之和,这种多样性的衡量标准为算法提供了灵活性。
4. 时间上的分离:如果正负传播可以在时间上分离,那么负传播可以离线进行,这使得正向传播中的学习过程更加简化。
首先,这里的正样本并不是我们常理解的分类算法里的正负样本的正样本。而是你训练集带有标签的样本,假设是二分类任务,这个正样本可以是0也可以是1。而这里的负样本就是非正样本的其他样本,都是负样本。可以自造假数据,也可以网络自身生成的假数据。比如在手写体数字MNIST识别中,将正确数字叠加掩码图片得到图片A,再找个非正确数字图片叠加(1-掩码的图片)得到B,再将A和B叠加,这就是负样本了,如下图所示。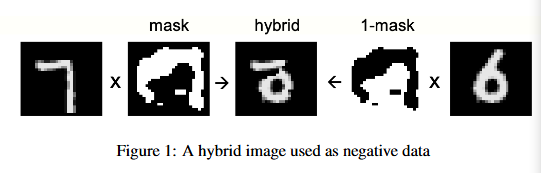
其次,了解了正负样本的含义,再看“优度”,论文给出了一种比较简单的函数,层活动平方和,即神经网络某一层的神经元输出的平方和:。然后,对优度减去1个固定值,使得对正样本都>0,对负样本<0。那以下面的概率作为目标函数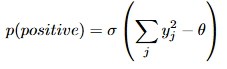
其实看到这里,想问目标函数为什么是这个?取值又是怎么确定?文中没有详细解释,我想了下,就是对正样本算上面的概率的时候,越大就越接近真实分布,对负样本越小越不是来自真实分布。毕竟负样本是你造出来的。那这个阈值怎么给呢?原文没有说明,搜了些资料说是0.01。
那网络权重该怎么更新呢?按以下公式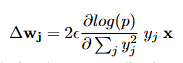
其中,是层归一化前ReLU的活动度,wj是神经元j传入权值的向量,ε是学习速率。在权值更新后,神经元j活动的变化只是标量积。在权重更新引起的活动变化中,唯一依赖于j的项是,所以所有隐藏的活动都以相同的比例变化,权重更新不会改变活动向量的方向。
我们知道,神经网络的一大特点就是反向传播,是沿着网络的路径一步步递推到最后的损失函数,再对损失函数进行求导,一层层反向传导求梯度,逐层调整参数。这是人为设计的过程,从理论上可以证明这个是有效且可行的,且符合机器学习的基本框架,但不一定是大脑的工作机制。而FF算法无需计算梯度,直接通过正向传递更新权重,计算量较小。正向传播可以并行化,适合大规模数据处理。
FF算法是一种新颖的训练方法,具有更好的生物合理性和低功耗特性,适合在边缘设备和实时学习场景中使用,所以对于现在的AI芯片的研发也有重要的研究意义。也许未来随着生物学上对大脑的工作机制和原理研究的深入,FF算法也许会被证明更接近于大脑的计算和学习模式,会是一项颠覆性的认知改变。现有的深度学习算法的训练框架会进一步被重塑。




